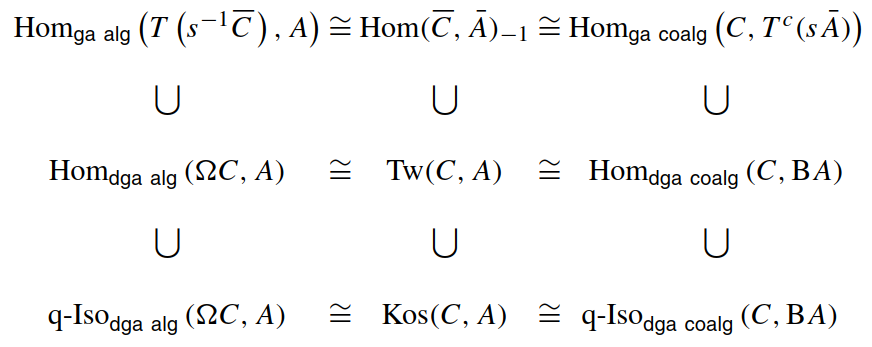
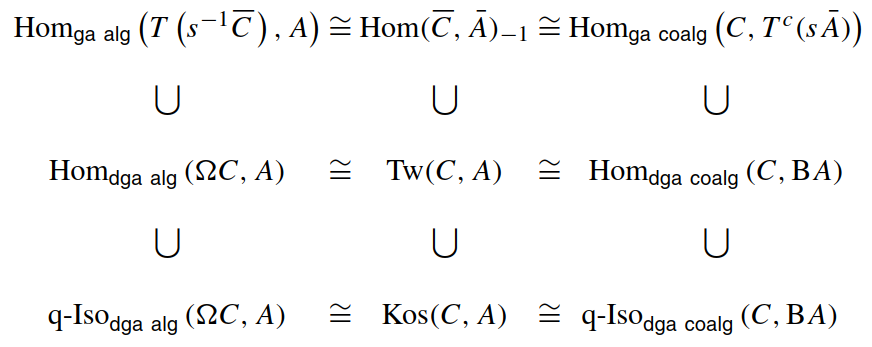
Time: Wednesdays 1:00 - 2:30 PM, unless otherwise noted.
Location: on Zoom.
The Zoom link will be emailed to members of the Department of Mathematics and Statistics. Please contact Martin Frankland if you would like to receive the announcements but are not a member of the department.
In this learning seminar, we will study differential graded (DG) algebras and their applications to rational homotopy theory.
The lecture series will be interspersed with guest research talks, which are posted on our Youtube channel.
| Date | Speaker | Title and abstract | References |
|---|---|---|---|
| Thursday January 21 4:30 PM |
Duncan Clark (Ohio State University) |
An intrinsic operad structure for the derivatives of the identity A long standing slogan in Goodwillie's functor calculus is that the derivatives of the identity functor on a suitable model category should come equipped with a natural operad structure. A result of this type was first shown by Ching for the category of based topological spaces. It has long been expected that in the category of algebras over a reduced operad $\mathcal{O}$ of spectra that the derivatives of the identity should be equivalent to $\mathcal{O}$ as operads. In this talk I will discuss my recent work which gives a positive answer to the above conjecture. My method is to induce a "highly homotopy coherent" operad structure on the derivatives of the identity via a pairing of underlying cosimplicial objects with respect to the box product. This cosimplicial object naturally arises by analyzing the derivatives of the Bousfield-Kan cosimplicial resolution of the identity via the stabilization adjunction for $\mathcal{O}$-algebras. Time permitting, I will describe some additional applications of these box product pairings including a new description of an operad structure on the derivatives of the identity in spaces. |
Recording |
| Thursday January 28 4:30 PM |
Niko Schonsheck (Ohio State University) |
Fibration theorems, functor calculus, and chromatic connections in $\mathcal{O}$-algebras By considering algebras over an operad $\mathcal{O}$ in one's preferred category of spectra, we can encode various flavors of algebraic structure (e.g. commutative ring spectra). Topological Quillen (TQ) homology is a naturally occurring notion of homology for these objects, with analogies to both singular homology and stabilization of spaces. In this talk, we will begin by discussing a fibration theorem for TQ-completion, showing that TQ-completion preserves fibration sequences in which the base and total $\mathcal{O}$-algebra are connected. We will then describe a few results that hint towards an intrinsic connection between TQ-completion and the convergence of the Taylor tower of the identity functor in the category of $\mathcal{O}$-algebras. Lastly, time permitting, we will discuss recent joint work with Crichton Ogle on the chromatic localization of the homotopy completion tower of $\mathcal{O}$-algebras and connections to functor calculus. |
Recording |
| February 3 | Don Stanley | DG-algebras and HZ-algebra spectra We will discuss the equivalence between differential graded (DG) algebras and algebras over the Eilenberg-MacLane spectrum HZ. |
|
| February 10 | Martin Frankland | The derived category of a DG-algebra We will describe the derived category of a DG-algebra as a triangulated category. It arises as the homotopy category of a model structure on DG-modules. We will tackle the question: When do two DG-algebras have equivalent derived categories? In stark contrast to the case of rings, for DG-algebras, the derived category does not determine the homotopy theory of DG-modules. |
B. Shipley, Morita theory in stable homotopy theory (2007). Notes from the talk |
| February 17 | Reading Week. No seminar. | ||
| February 24 | Larry So | Topological equivalences for DG-algebras I will talk about topological equivalence between DG-algebras and look at the difference between topological equivalence and quasi-isomorphism. |
D. Dugger and B. Shipley, Topological equivalences for differential graded algebras (2007). Notes from the talk |
| March 3 | Matthew Alexander | $A_{\infty}$ algebras and Kadeishvili's theorem $A_{\infty}$ algebras are introduced in the context of cochain complexes. Motivation for the defining equations of $A_{\infty}$ algebras is provided before it is demonstrated that $A_{\infty}$ algebras can be viewed as coderivations on a tensor coalgebra. Finally, a sketch of Kadeishvili's theorem is provided, showing that the cohomology of differential graded algebras admits an $A_{\infty}$ algebra structure quasi-isomorphic to the DG-algebra. |
|
| March 10 | Don Stanley | Commutative DG-algebras and rational homotopy theory Rational homotopy theory is modeled by the homotopy theory of (graded) commutative DG-algebras (CDGAs). We introduce the notion of rational equivalence of spaces, and then develop the theory of CDGAs. We start with some basic standard notation for CDGAs and then discuss equivalences and formality. We describe a number of examples of CDGAs and maps between them. Looking at the role of cofibrancy, we describe the difference between CDGAs and DGAs and finish with an example of a non-formal CDGA. |
Notes from the talk |
| March 17 | Martin Frankland | Polynomial differential forms and Sullivan's theorem I will explain how (graded) commutative DG-algebras (CDGAs) model rational homotopy theory. The functors in both directions are: the PL de Rham complex of a simplicial set, and the spatial realization of a CDGA. I will describe the model structure on rational CDGAs, which is not available in positive characteristic. Then I will sketch why the two functors induce an equivalence of homotopy categories when restricted to simply-connected objects. |
K. Hess, Rational homotopy theory: a brief introduction (2007). Notes from the talk |
| March 24 | Arnaud Ngopnang Ngompe | Applications of Sullivan minimal models In this seminar talk, we give some examples of minimal models together with some computations using them. These computations include the rational homotopy groups of spheres and the rational cohomology of Eilenberg-MacLane spaces. |
J. Moerman, Rational Homotopy Theory (2015). Notes from the talk |
| March 31 | Larry So | Models for homotopy fibers and pullbacks I will talk about the Sullivan models for homotopy fibers and pullbacks, and look at the rational cohomology of loop spaces of simply connected spaces. |
Notes from the talk |
| April 7 | Don Stanley | Quillen Lie models We introduce differential graded Lie algebras and the Quillen model for rational homotopy theory, and do a few examples. We will also describe a connection with the Adams-Hilton model and Milnor-Moore's work on the homology of loop spaces and rational homotopy groups. |
|
| April 14 | Martin Frankland | Computing Whitehead products using Sullivan minimal models I will explain how a Sullivan minimal model of a space encodes the Whitehead product on rational homotopy groups, namely as the dual of the quadratic part of the differential. I will look at a few examples and computations. |
Y. Félix, S. Halperin, and J.C. Thomas, Rational Homotopy Theory (2001). Notes from the talk |

For more information, contact Martin Frankland.