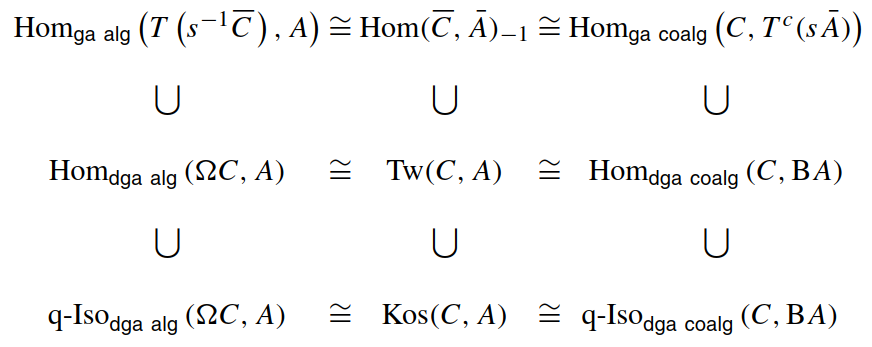
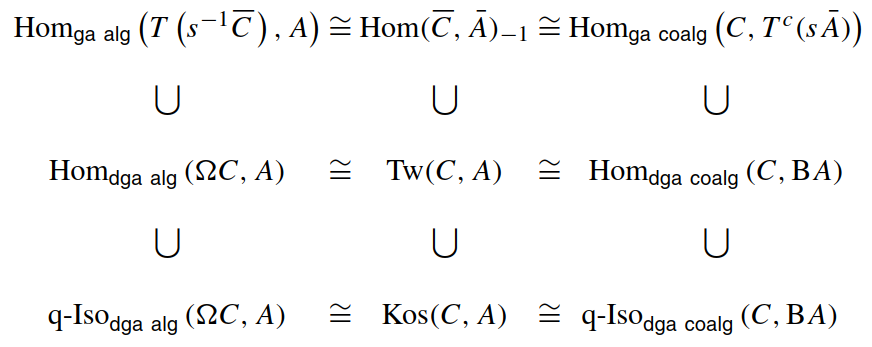
Time: Wednesdays 11:30 AM - 1:00 PM, unless otherwise noted.
Location: on Zoom.
The Zoom link will be emailed to members of the Department of Mathematics and Statistics. Please contact Martin Frankland if you would like to receive the announcements but are not a member of the department.
In this learning seminar, we will study differential graded (DG) algebras. We will discuss some algebraic aspects, some applications to topology, and connections with homotopy theory.
The lecture series will be interspersed with guest research talks, which are posted on our Youtube channel.
| Date | Speaker | Title and abstract | References |
|---|---|---|---|
| September 9 | Don Stanley | An introduction to differential graded algebras Starting from graded modules and chain complexes, we introduce the category of differential graded algebras (DGAs). |
Notes from the talk |
| September 16 | Martin Frankland | Homology and quasi-isomorphisms I will discuss the homology of a DGA as well as quasi-isomorphisms, which provide a notion of equivalence between two DGAs. |
Notes from the talk |
| September 23 | Martin Frankland | Examples of differential graded algebras I will present a few examples of DGAs coming from algebra, topology, and geometry. |
Notes from the talk |
| September 30 | Don Stanley | Massey products We discuss tensor algebras and symmetric algebras equipped with differentials, then we introduce Massey products and time permitting the endomorphism algebra of a chain complex. |
Notes from the talk |
| October 7 | Katharine Adamyk (University of Western Ontario) |
Classifying stable modules over A(1) This talk will present a classification theorem for a certain class of modules over A(1), a subalgebra of the mod-2 Steenrod algebra. In order to give the module classification, there will be some background on Margolis homology (an invariant of modules over the Steenrod algebra) and the stable module category. Applications of the classification theorem to lifting A(1)-modules to modules over the Steenrod algebra and applications to the computation of certain localized Adams spectral sequences will also be discussed. |
Recording |
| October 14 | Tse Leung So | The bar and cobar constructions We will look at the definitions of the bar and cobar constructions, some examples and their adjointness relation. |
Notes from the talk |
| October 21 | Tse Leung So | The Eilenberg-Moore spectral sequence I will talk about the Tor functor and Eilenberg-Moore spectral sequences. |
Notes from the talk |
| October 28 | Arnaud Ngopnang Ngompe | Model structures on DG-modules and DG-algebras We describe a cofibrantly generated model structure on DG-modules which induces a model structure on DG-algebras as the category of monoids in DG-modules. |
Slides from the talk |
| November 4 4:30 - 5:30 PM |
Yu Zhang (Nankai University) |
Koszul duality and TQ-homological Whitehead theorem of structured ring spectra Quillen's work on rational homotopy theory illustrates the duality between differential graded Lie algebras and differential graded cocommutative coalgebras. In homotopy theory, there is an analogous duality phenomenon, called Koszul duality, where the role of differential graded algebras is played by structured ring spectra. In this talk, I will talk about Koszul duality as well as some of my related recent work on Topological Quillen (TQ) localization and the homological Whitehead theorem of structured ring spectra. This is joint with John E. Harper. |
Recording |
| November 11 | Reading Week. No seminar. | ||
| November 18 | Martin Frankland | Derived Morita equivalence Two rings are called Morita equivalent if their categories of modules are equivalent. We will review Morita's classic theorem providing a criterion for when that happens. We will then consider the question: When do two rings have equivalent derived categories? Rickard's theorem provides an answer. Lastly, we will look at the derived category of a DG-algebra and tackle the question: When do two DG-algebras have equivalent derived categories? |
S. Schwede, Morita theory in abelian, derived and stable model categories (2004). Notes from the talk |
| November 25 | Matthew Alexander | The stable Dold-Kan correspondence We will develop background on symmetric spectra and the smash product of spectra. After introducing Eilenberg-MacLane (EM) spectra, the talk will culminate with a sketch of the proof of the stable Dold-kan correspondence between EM-module spectra and unbounded chain complexes. |
S. Schwede, B. Shipley, Stable model categories are categories of modules (2003). Notes from the talk |
| December 2 | Tse Leung So | Monoidal Dold-Kan correspondence We will see how to get a Quillen equivalence between simplicial algebras and connective DG-algebras from the functors in the Dold-Kan correspondence. |
S. Schwede, B. Shipley, Equivalences of monoidal model categories (2003). Notes from the talk |

For more information, contact Martin Frankland.