Time: Wednesdays 3:30 - 5:00 PM, unless otherwise noted.
Location: ED 612.
The lecture series on functor calculus will be interspersed with research talks on other topics.
| Date | Speaker | Title and abstract | References |
|---|---|---|---|
| September 19 | Don Stanley | Metrics on persistence modules Persistence modules are an important tool in data analysis. We look at various metrics on the space of persistence modules (and generalized persistence modules) and describe the relationships between them. In this talk before giving our results we will give some motivation and an introduction to persistence modules. This is joint work with Peter Bubenik and Jonathan Scott. |
|
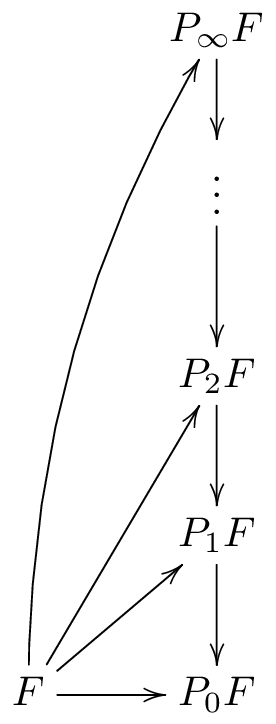
| September 26 | Martin Frankland | Foundations of functor calculus I will present Goodwillie's foundational work on calculus for homotopy functors from spaces to spaces or spectra. There is a notion of n-excisive functor, and a functor admits a universal n-excisive approximation $F \to P_n F$. As n varies, these fit into a tower called the Taylor tower of the functor F. The notion of analyticity gives conditions under which a functor is well approximated by its Taylor tower. I will briefly discuss a motivational application to Waldhausen K-theory of spaces. |
T. Goodwillie, Calculus III: Taylor series, Geom. Topol. 7 (2003). |
| October 3 | Martin Frankland | Foundations of functor calculus, Part 2 The layers of the Taylor tower are homogeneous functors. I will describe the classification of homogeneous functors. This leads to the notion of derivatives of a functor, which are spectra with a symmetric group action. I will also discuss some examples of Taylor towers. |
|
| October 10 | Paul Arnaud Songhafouo Tsopméné | Bar construction for topological operads and the Goodwillie derivatives of the identity An operad is an algebraic structure that models the properties (associativity, commutativity and other relations) of an algebra. Roughly speaking, an element of an operad is an operation with many inputs and one output. Operads have found many applications in different areas, such as in deformation quantization of Poisson manifolds, graph homology in the work of Maxim Kontsevich and Thomas Willwacher, Functor calculus of Goodwillie... This talk will focus on this latter area. I will discuss the bar construction for topological operads, which is useful to construct an operad structure on the derivatives of the identity functor on the category of based spaces. |
M. Ching, Bar constructions for topological operads and the Goodwillie derivatives of the identity, Geom. Topol. 9 (2005). |
| October 17 | No seminar. | ||
| October 24 | José Carrasquel Vera | Sectional category à la Quillen In this talk we will develop some new rational homotopy theory techniques and show how they can be used to estimate sectional categories such as topological complexity and Lusternik-Schnirelmann category through the prism of Quillen models. We will also show how this approach can be used to address some open problems. |
|
| October 31 | Paul Arnaud Songhafouo Tsopméné | Bar construction for topological operads and the Goodwillie derivatives of the identity, Part 2 I will continue discussing the operad structure on the derivatives of the identity functor on the category of based spaces. |
|
| November 7 | Fall Break. No seminar. | ||
| November 14 | No seminar today. | ||
| November 21 | No seminar today. | ||
| November 28 | No seminar today. | ||
| December 5 | No seminar today. | ||
| December 12 | Paul Arnaud Songhafouo Tsopméné | Cosimplicial models for manifold calculus Manifold calculus is a tool developped by Goodwillie and Weiss which enables to approximate a contravariant functor, F, from the category of m-manifolds to the category of spaces (or alike), by its "Taylor approximation", T∞F. I will explain how to construct a fairly explicit and computable cosimplicial model of T∞F(M) out of a simplicial model of the manifold M (i.e. out of a simplicial set whose realization is M). This cosimplicial model in degree p is then equivalent to the evaluation of F on a disjoint union of as many m-disks as p-simplices in the simplicial model of M. |
For more information, contact Martin Frankland.