Welcome to My home page!


I am a professor of mathematics at the University of Regina, Canada.



CONTACT

Department of Mathematics and Statistics
University of Regina
Regina SK
Canada S4S 0A2
office: College West 307.1
e-mail: liviu.mare@gmail.com

 
A GLIMPSE INTO MY RESEARCH

My research interests are motivated by geometry, which is a branch of mathematics that originates in the study of objects in the surrounding world in terms of their shape, size, and relative position. One can say more about such objects if they posses some symmetry: for instance, one can say more about an isosceles or an equilateral triangle than about an arbitrary one.

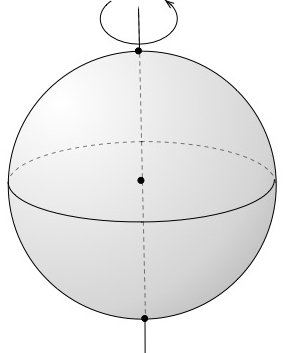A sphere is also a very symmetric object. For example, imagine that the sphere you see in the diagram rotates around the diameter and you watch it: you won't notice any difference. In the modern language of mathematics we say that the sphere is acted on by the circle, which is a group.
Differentiable manifolds are used to model objects of a world that has dimension two, three, or even larger. Their symmetry properties are expressed in terms of differentiable group actions on manifolds. A central question in this context concerns the impact that the symmetry (i.e. group action) has on the shape of the manifold. This question can be addressed at several levels, depending on how precise the required information about the shape is: from less accurate, when only the topology matters, to very accurate, when even a certain supplementary structure, e.g. Riemannian or symplectic, is involved. A related notion arises by considering vector spaces with group actions that preserve the linear structure: their study is called representation theory. In spite of its algebraic appearance, this theory turns out to be a useful tool in geometry. [For more technical details follow the research link above or click here.]