Social Studies 201

March 30, 2001

Answers to Problem Set 4

Click here for answers to problems 1-3.

4. (a) Interval Estimates from MINITAB

MTB > TInterval 95.0 'v4' 'v9' 'income'.

N MEAN STDEV SE MEAN 95.0 PERCENT C.I.

v4 372 3.0860 1.3943 0.0723 ( 2.9438, 3.2282)

v9 372 3.4758 1.0925 0.0566 ( 3.3644, 3.5872)

income 372 65.69 43.47 2.25 ( 61.25, 70.12)

MTB > TInterval 80.0 'v4' 'v9' 'income'.

N MEAN STDEV SE MEAN 80.0 PERCENT C.I.

v4 372 3.0860 1.3943 0.0723 ( 2.9932, 3.1788)

v9 372 3.4758 1.0925 0.0566 ( 3.4031, 3.5485)

income 372 65.69 43.47 2.25 ( 62.79, 68.58)

MTB > TInterval 99.0 'v4' 'v9' 'income'.

N MEAN STDEV SE MEAN 99.0 PERCENT C.I.

v4 372 3.0860 1.3943 0.0723 ( 2.8988, 3.2732)

v9 372 3.4758 1.0925 0.0566 ( 3.3291, 3.6225)

income 372 65.69 43.47 2.25 ( 59.85, 71.52)

(b) Comments

(i) For the 99% interval for V4, the calculations are as follows, with the sample standard deviation s being used as an estimate of the true standard deviation s:

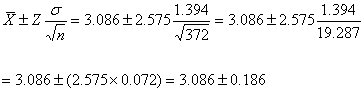
and the interval is from 2.900 to 3.271. This is slightly different from the interval shown of (2.8988, 3.2732), most likely due to rounding differences.

(ii) For any given confidence level, the Z values are the same and the sample sizes are the same. After this, the only reason why the intervals would have different width is that the standard deviations of the respective populations, or their estimates from the samples, differ. For example, for 99% confidence, for V4 the width is 3.27-2.90=0.37 while for

V9 the width is 3.62-3.33=0.29. The interval for V4 is wider because the estimate of the standard deviation for V4 is 1.39, while the sample standard deviation is only 1.09 for V9.

(iii) In the case of any given variable, the intervals of different confidence level differ because the appropriate Z value is different. For 80% confidence, Z=1.28, for 95% confidence, Z=1.96, and for 99% confidence, Z=2.575. For higher confidence levels, the Z values are larger, so the intervals are wider.

(iv) There is only very limited support for the claim that the mean income could be $60,000. The 80% and 95% per cent intervals do not contain the $60,000 value for income, although the 99% interval does, at very close to the lower limit of the interval. Since $60,000 is not in the other two intervals, it seems unlikely that income would be this low. It takes a very high confidence level, 99% confidence level with Z=2.575, before an interval wide enough to include $60,000 results. A researcher would conclude that the income is very likely higher than $60,000, even though this cannot be stated definitively.