Social Studies 201

Fall, 2000

Final Examination

9 a.m. – 12 noon, Friday, December 8, 2000, CL410.

Answer any three (3) questions.

1. Student Debt Load. The data in Table 1 come from the Survey of Student Attitudes and Experiences, Fall 1998. Use these data to test and comment on the following assertions.

a. A student advocate claims that university funding has been cut so that that university student debt loads increased by over $5,000 in one year. Test at the 0.10 level of significance.

b. A politician from the North West Party claims that there was no crisis in university funding since over two-thirds of students had no increase in debt load in 1998-1999. Test at the 0.05 level of significance.

c. The local legislative member from the Centre Party of Government says that her party has done a lot to help students, with the result that student debt loads increased by $1,500 during 1998-1999. Test at the 0.10 level of significance.

d. What might you conclude about debt loads from the above tests and the data in Table 1.

Table 1. Change in Debt of University of Regina Undergraduates, 1998-1999

Change in Debt During 1998-1999 (in dollars)	Number of Students
Less than 0	10
0	397
0-2,499	38	For those whose debt increased, the mean increase was $5,275 with a standard deviation of $3,689 .
2,500-4,999	39
5,000-9,999	68
10,000 plus	22
Total	574
Mean	1,511
Standard Deviation	3,132

2. Views on Multiculturalism. Two attitude questions on multiculturalism of a sample of University of Regina undergraduates in the Survey of Student Attitudes and Experiences, Fall 1998 gave the results in Table 2.

Table 2. Responses to Questions on Multiculturalism

Response	Number of Respondents
	Diversity Fundamental	Fund Festivals
Strongly disagree – 1	9	92
Disagree – 2	25	150
Neutral – 3	136	198
Agree – 4	241	145
Strongly agree – 5	285	109
Total	696	695
Mean	4.10	3.05
sd	0.92	1.27

a. Using the numerical coding of the responses shown in the first column of Table 2, calculate the mean and standard deviation of the response to each of the two questions.

b. What are the 90% and 98% interval estimates for the true mean responses to each of these questions for all University of Regina undergraduates?

c. Compare the two distributions and comment on what the two interval estimates say about the responses to these two questions.

3. In the November 27, 2000 federal election, 301 seats were contested. The Liberal party received 40.8 % of the popular vote and obtained 172 seats while the Canadian Alliance received 25.5% of the vote and obtained only 66 seats.

a. If the chance of the Canadian Alliance winning any seat is 25.5%, use the normal approximation to the binomial to find the probability that the Canadian Alliance would obtain 66 or fewer seats.

b. Suppose that you regard the 301 seats as a sample, and the chance of a Liberal winning any seat is equal to the Liberal percentage of the popular vote. What is the 99% interval estimate for the proportion of the 301 seats the Liberals would obtain?

c. Compare the results in a. and b. with the actual number of seats each of these two parties obtained and explain why the binomial does not appear adequate as an explanation of the distribution of seats in the federal parliament.

4. The data in Table 3 represent the responses to the question “Should the first priority of government be to use the surplus to cut income taxes, increase spending on programs like health care and education, or reduce the government debt?” The data were produced from an October, 2000 poll by Decima Research Inc., conducted for the Canadian Association of University Teachers.

Table 3. Responses to Question on Use of Surplus. Manitoba, Saskatchewan, Alberta, and Canada.

Response	Manitoba/Saskatchewan	Alberta	Canada
Cut income taxes	28	40	428
Increase spending on programs such as health care and education	72	75	1,058
Reduce government debt	38	66	496
Total	138	181	1,982

a. Obtain 95% interval estimates for the proportion of responses from each of the three areas that say the first priority should be to increase spending on programs like health and education.

b. Test the hypothesis that more than 50% of the population of the Manitoba/Saskatchewan region support increased spending for programs such as health care and education. Conduct the same test for Canada as a whole.

c. Write a short note describing the results of the interval estimates and hypothesis tests, commenting on the similarities or differences in response among the regions.

5. a. The attached page Decima Express Methodology comes from the same survey as that noted in question 4. Using the formulae for interval estimates for proportions, obtain what Decima calls the “error intervals” for Manitoba/Saskatchewan, Alberta, and Canada. What is missing from Decima’s description of the error intervals?

b. What would be the sample size required in Saskatchewan in order to achieve an interval no more than 2 percentage points wide, with 90% confidence?

c. From Table 3, obtain the 99% interval estimates for the proportion of Manitoba/Saskatchewan residents who support reducing the government debt? Why is this interval wider than Decima’s “error interval” for Manitoba/Saskatchewan?

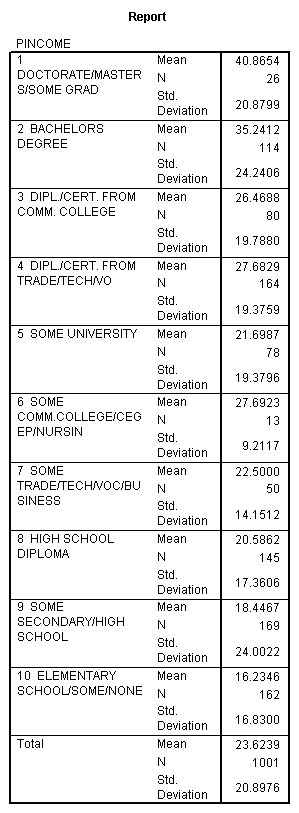
6. The data in Table 4 come from the Saskatchewan respondents to Statistics Canada’s General Social Survey, Cycle 11, 1996. For each category of education, the table gives the mean annual income (in thousands of dollars), the sample size (N), and the standard deviation of annual income (in thousands of dollars). Use these data to answer the following.

a. Obtain the 95% confidence interval for the true mean annual income for all Saskatchewan adults with (i) a diploma or certificate from a community college (category 3), and (ii) a bachelors degree (category 2).

b. Test whether the mean annual income of all Saskatchewan adults with (i) a bachelors degree exceeds $30,000, and (ii) a diploma or certificate from a community college is less than $30,000. Are these results consistent with what you found in a?

c. How large a sample size of those with a doctorate/masters/some graduate work (category 1) would be required in order to obtain the true mean annual income correct to within plus or minus $2,500? (90% confidence).

Table 4. Means, Standard Deviations, and Sample Sizes (N) of Personal Income Annually (in thousands of dollars) of Saskatchewan Adults in the 1996 General Social Survey, Classified by Education Level